Tutorial QE: Criando arquivos de input

Construindo o input básico para rodar um cálculo

Vamos agora montar um input para um cálculo SCF (Self-Consistent Field) utilizando o programa pw.x da suíte do Quantum ESPRESSO. Existem diversos parâmetros que podem ser alterados no input do pw.x, e todos eles estão listados e explicados aqui.

Abaixo você encontrará um exemplo básico do input para um cálculo SCF para o grafeno.

&control
   calculation = '$CALC' ,
   restart_mode = 'from_scratch' ,
   wf_collect = .false. ,
   outdir = '.' ,
   pseudo_dir = '$PSEUDO_DIR' ,
   prefix = '$PREFIX' ,
/
&system
   ibrav = 0 ,
   nat =  2 ,
   ntyp = 1 ,
   ecutwfc = 100.0 ,
   ecutrho = 1200.0 ,
/
&electrons
   conv_thr =  1.0D-10 ,
   electron_maxstep = 1000 ,
/
ATOMIC_SPECIES
   C   12.0107  C.pbe-van_ak.UPF
CELL_PARAMETERS (angstrom)
  2.466063858   0.000000000   0.000000000
  1.233031929   2.135673950   0.000000000
  0.000000000   0.000000000  20.000000000
ATOMIC_POSITIONS (angstrom)
C        3.082579823   1.779728292   3.220971257
C        0.616515965   0.355945658   3.220971257
K_POINTS automatic
  21 21 1   0 0 0

O input para o cálculo é relativamente simples. Ele é composto de cinco principais seções: control, system e electrons, ions e cell que controlam os parâmetros principais do cálculo. Todas as seções principais devem apresentar um \& na frente, caso contrário o programa irá apresentar um erro.

A seção &control apresenta os controles gerais do cálculo. Nela podemos controlar:

• calculation: O tipo de cálculo a ser executado. Pode ser ‘scf’, ‘nscf’, ‘bands’, relax, vc-relax, md ou vc-md;
• restart_mode: A forma como o cálculo inicia: do zero (‘from_scratch’) ou reiniciando um outro cálculo (‘restart’);
• wf_collect: Se iremos salvar as funções de onda (.true.) ou não (.false.). Em geral as funções de onda são arquivos muito pesados (na casa dos GBytes), portanto só iremos salvar as funções de onda em casos muito específicos;
• outdir:O diretório onde o programa ira salvar todos os arquivos temporários do cálculo. O ‘.’ significa que o pw.x salvará qualquer arquivo temporário no mesmo diretório em que o cálculo está sendo submetido.
• pseudo_dir: O diretório que contém os arquivos dos pseudopotenciais.
• prefix: O prefixo do cálculo. Todos os cálculos sequenciais precisam apresentar o mesmo prefixo.

A seção &system apresenta os controles do sistema que executaremos o cálculo. Nela podemos controlar:

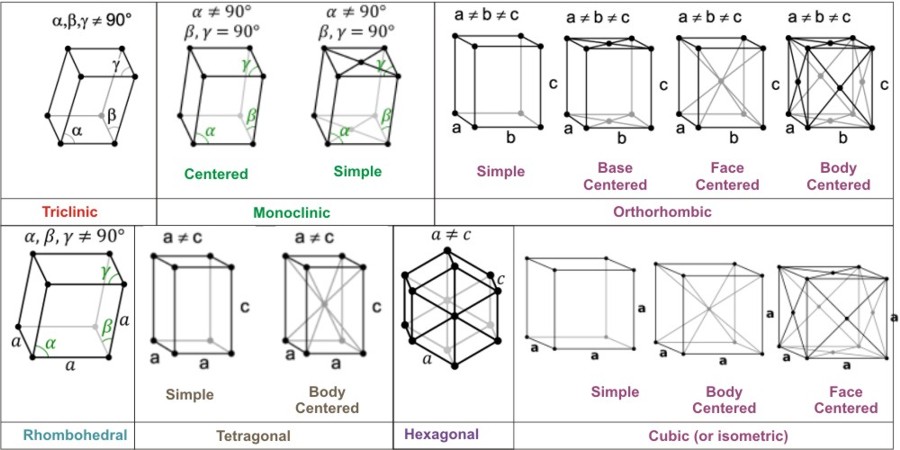
• ibrav: O tipo de célula unitária. Se ibrav=0 o programa lê os dados passados manualmente na caixa CELL_PARAMETERS, no fim do arquivo. Caso desejemos montar um sistema que se encaixe em uma das redes de Bravais, podemos informar qual rede é especificamente aqui. Nesse caso deve ser adicionado também a opção celldm(1)=a, onde a é o maior parâmetro da célula, em unidades de atômicas (1 Å = 1.88973 bohr).

  • 1 = Cúbico primitivo P: \(v_1\) = a(1,0,0), \(v_2\) = a(0,1,0), \(v_3\) = a(0,0,1)
  • 2 = Cúbico de face centrada F (fcc): \(v_1\) = (a/2)(-1,0,1), \(v_2\) = (a/2)(0,1,1), \(v_3\) = (a/2)(-1,1,0)
  • 3 = Cúbico de corpo centrado I (bcc): \(v_1\) = (a/2)(1,1,1), \(v_2\) = (a/2)(-1,1,1), \(v_3\) = (a/2)(-1,-1,1)
  • 4 = Hexagonal e Trigonal P: celldm(3)=c/a, \(v_1\) = a(1,0,0), \(v_2\) = a(-1/2,sqrt(3)/2,0), \(v_3\) = a(0,0,c/a)
  • 5 = Trigonal R: celldm(4)=cos(gamma), \(v_1\) = a(tx,-ty,tz), \(v_2\) = a(0,2ty,tz), \(v_3\) = a(-tx,-ty,tz)
  • 6 = Tetragonal Primitivo P: celldm(3)=c/a, \(v_1\) = a(1,0,0), \(v_2\) = a(0,1,0), \(v_3\) = a(0,0,c/a)
  • 7 = Tetragonal de corpo centrado I (bct): celldm(3)=c/a, \(v_1\) = (a/2)(1,-1,c/a), \(v_2\) = (a/2)(1,1,c/a), \(v_3\) = (a/2)(-1,-1,c/a)
  • 8 = Ortorrômbico P: celldm(2)=b/a, celldm(3)=c/a, \(v_1\) = (a,0,0), \(v_2\) = (0,b,0), \(v_3\) = (0,0,c)
  • 9 = Ortorrômbico de base centrada (bco): celldm(2)=b/a, celldm(3)=c/a, \(v_1\) = (a/2, b/2,0), \(v_2\) = (-a/2,b/2,0), \(v_3\) = (0,0,c)
  • 10 = Ortorrômbico de face centrada: celldm(2)=b/a, celldm(3)=c/a, \(v_1\) = (a/2,0,c/2), \(v_2\) = (a/2,b/2,0), \(v_3\) = (0,b/2,c/2)
  • 11 = Ortorrômbico de corpo centrado: celldm(2)=b/a, celldm(3)=c/a, \(v_1\) = (a/2,b/2,c/2), \(v_2\) = (-a/2,b/2,c/2), \(v_3\) = (-a/2,-b/2,c/2)
  • 12 = Monoclínico P, eixo único c: celldm(2)=b/a, celldm(3)=c/a, celldm(4)=cos(ab), \(v_1\) = (a,0,0), \(v_2\) = (bcos(gamma),bsin(gamma),0), \(v_3\) = (0,0,c)
  • 13 = Monoclínico de base centrada: celldm(2)=b/a, celldm(3)=c/a, celldm(4)=cos(gamma), \(v_1\) = (a/2,0,-c/2), \(v_2\) = (bcos(gamma), bsin(gamma), 0), \(v_3\) = (a/2, 0, c/2)
  • 14 = Triclínico: celldm(2)= b/a, celldm(3)= c/a, celldm(4)= cos(bc), celldm(5)= cos(ac), celldm(6)= cos(ab)
• nat: Número total de átomos na célula unitária;
• ntyp: Número de tipos de átomos diferentes;
• ecutwfc: Energia de corte das funções de onda em Ry;
• ecutrho: Energia de corte da densidade de carga.

A seção &electrons controla os parâmetros de convergência do cálculo autoconsistente:

• conv_thr: Limite de convergência para autoconsistência. Padrão: \(10^{-6}\), Valor sugerido: \(10^{-8}\) ou \(10^{-10}\). Parâmetro mais apertado: \(10^{-12}\).
• electron_maxstep: Número máximo de iterações antes de o programa cancelar o calculo por não-convergência.

As seções &ions e &cell controlam os parâmetros de movimentação dos átomos e dos parâmetros de célula. Eles são opcionais para cálculos autoconsistentes, sendo somente necessários para cálculos em que ocorre o relaxamento da estrutura atômica e/ou dos parâmetros de célula.

Todas as seções são iniciadas com o símbolo & e devem ser finalizadas com uma barra. Além disso o nome dessas tags deve ser escrito em letra minúscula.

Em seguida, começam as tags específicas do sistema que será calculado. Todas essas tags são escritas em letras maiúsculas, sem & ou barra.

A tag ATOMIC_SPECIES é onde descreveremos os diferentes átomos, sua massa e o tipo de pseudopotencial a ser utilizado. Os nomes dos pseudopotenciais seguem um uma convenção: simbolo_atomico.descrição.UPF onde descrição= [campo1-][campo2-]campo3-[campo4-]campo5[_campo6]

• campo1 (opcional) = rel: pseudopotencial full-relativistic
• campo2 (opcional) = starNl: um core-hole por estado Nl ou starhNl: meio core-hole por estad Nl
• campo3 = tipo de funcional de troca-correlação:
  • pz: Perdew-Zunger (LDA) exch-corr
  • vwn: Vosko-Wilk-Nusair (LDA) exch-corr
  • pbe: Perdew-Burke-Ernzerhof (PBE) exch-corr
  • blyp: Becke-Lee-Yang-Parr (BLYP) exch-corr
  • pw91: Perdew-Wang 91 gradient-corrected functional
  • tpss: Tao-Perdew-Staroverov-Scuseria (TPSS) meta-GGA
  • coulomb: Coulomb bare -Z/r potential
• campo4 (opcional) = qualquer combinação de estados:
  • s: semicore state s in valence
  • p: semicore state p in valence
  • d: semicore state d in valence
  • f}: valence f state in core
  • n: nonlinear core-correction
• campo5 = Método de construção do pseudopotencial:
  • ae: All-Electron (no pseudization)
  • mt: Martins-Troullier
  • bhs: Bachelet-Hamann-Schlueter and derived
  • vbc: Von Barth-Car (direct fit)
  • van: Vanderbilt ultrasoft
  • rrkj: Rappe Rabe Kaxiras Joannopoulos (norm-conserving)
  • rrkjus: Rappe Rabe Kaxiras Joannopoulos (ultrasoft)
  • kjpaw: Projector Augmented Wave (Kresse-Joubert paper)
  • bpaw: Projector Augmented Wave (original Bloechl recipe)
• campo6 (opcional): Qualquer identificação da versão do pseudopotencial. Em geral é uma sequência de números.

A tag CELL_PARAMETERS é usada para descrever os parâmetros da célula primitiva quando ibrav=0. Pode ser nas unidades: { alat=a | bohr | crystal | angstrom | crystal_sg }.

A tag ATOMIC_POSITIONS é utilizada para descrever as posições dos átomos na célula unitária. Pode ser nas unidades: { alat=a | bohr | angstrom }.

A tag K_POINTS é utilizada para descrever o mesh de k-points que será utilizado para realizar o cálculo. Pode ser escolhido um mesh uniforme de k-points que será construído automaticamente seguindo o esquema proposto por Monkhorst–Pack [1]. Nesse caso deve ser dar também os valores: nk1, nk2, nk3, k1, k2, k3. Onde nk1, nk2 e nk3 são o número de kpoints nos eixos x, y e z e k1, k2 e k3 são os possíveis deslocamentos do centro da zona de Brilluin (\(\Gamma\)). Veremos mais sobre isso em breve.

[1] MONKHORST, Hendrik J.; PACK, James D. Special points for Brillouin-zone integrations. Physical review B, v. 13, n. 12, p. 5188, 1976. PDF