Tutorial QE: Sistemas moleculares (0D) - Parte 1

---

Nesse tutorial aprenderemos:

• Como obter valores de energia total em função da distância em moléculas diatômicas homonucleares;
• Como utilizar diferentes funções para modelar a superfície de energia potencial (SEP);
• Como obter informações fisico-químicas da molécula com base no modelo da SEP;

---

A superfície de Energia Potencial

Geralmente quando desejamos fazer qualquer tipo de cálculo com determinada estrutura, desejamos que ela esteja em seu estado de equilíbrio, i. e. as forças entre os átomos são as menores possíveis e a energia total é um mínimo na superfície de potencial. Mesmo quando desejamos fazer cálculos com um material que já possui sua estrutura determinada por difração de raios-X ou por RMN, em geral precisamos otimizar a estrutura para o nível em que estamos fazendo o cálculo. Existem algumas maneiras de fazer esse processo de otimização, que em geral se resume a determinar a superfície de energia potencial dos íons e procurar, nessa superfície, por mínimos globais. Para casos simples, veremos que podemos fazer esse processo manualmente. Já para casos mais complexos recorreremos a algoritmos poderosos para procurar esse mínimo de maneira automatizada.

Para explorar esse conceito vamos olhar para um caso simples, que apesar de não ser periódico é bastante instrutivo: A molécula de \(N_2\). Experimentalmente observa-se que o comprimento da ligação dessa molécula é de 1.0975 Å [1]. Vamos ver então se conseguimos obter em nível DFT-PBE/PW o valor do comprimento de ligação para essa molécula.

Para isso, crie um script de submissão como o abaixo. Execute o cálculo editando a variável D_NN, modificando posição do segundo átomo de nitrogênio seguindo os valores: 0.76825, 0.78142, 0.79459, 0.80776, 0.82093, 0.8341 , 0.84727, 0.86044, 0.87361, 0.88678, 0.89995, 0.91312, 0.92629, 0.93946, 0.95263, 0.9658 , 0.97897, 0.99214, 1.00531, 1.01848, 1.03165, 1.04482, 1.05799, 1.07116, 1.08433, 1.0975, 1.11067, 1.12384, 1.13701, 1.15018, 1.16335, 1.17652, 1.18969, 1.20286, 1.21603, 1.2292 , 1.24237, 1.25554, 1.26871, 1.28188, 1.29505, 1.30822, 1.32139, 1.33456, 1.34773, 1.3609 , 1.37407, 1.38724, 1.40041, 1.41358, 1.42675. Dessa forma, podemos construir a curva de energia potencial fazendo um gráfico da energia total em função da distância de ligação entre os átomos \(d_{N-N}\). Caso você rode esse cálculo em um sistema de cluster com Slurm ou PBS, não se esqueça de colocar a parte inicial do script como ensinado no Tutorial QE: Criando Scripts de Submissão.

Você precisará fazer o download do pseudo-potencial nesse site. Edite a variável PSEUDO_DIR para que seja o diretório no qual você salvou o pseudo-potencial. Edite a variável CMD_PW para o diretório no qual você compilou o QE.

D_NN='0.878'
PREFIX="n2_$D_NN"
PSEUDO_DIR="/home/pseudo"
CALC="scf"
CMD_PW="mpirun -np 4 /home/interlab/qe/bin/pw.x"

#Make SCF calculation
cat>$PREFIX.$CALC.in<<EOF
 &control
  calculation = '$CALC' ,
  restart_mode = 'from_scratch' ,
  wf_collect = .false. ,
  outdir = '.' ,
  pseudo_dir = '$PSEUDO_DIR' ,
  prefix = '$PREFIX' ,
 /
 &system
  ibrav = 1 ,  celldm(1) = 20
  nat =  2 ,  ntyp = 1 ,
  ecutwfc = 80.0 , ecutrho = 600.0 ,
 /
 &electrons
 conv_thr =  1.0D-10 , electron_maxstep = 5000 ,
 /
ATOMIC_SPECIES
  N    14.0107       N.pbesol-n-rrkjus_psl.1.0.0.UPF
ATOMIC_POSITIONS (angstrom)
  N        0.000000000   0.000000000   0.000000000
  N        $D_NN         0.000000000   0.000000000
K_POINTS automatic
	1 1 1   0 0 0
EOF
$CMD_PW < $PREFIX.$CALC.in > $PREFIX.$CALC.out

Como o primeiro átomo de nitrogênio está na origem, a posição do segundo átomo nos dará exatamente o tamanho da ligação. Perceba que estamos fazendo o cálculo para uma molécula isolada, entretanto o QE lida com sistemas periódicos. Para que possamos fazer o cálculo sem menores problemas, vamos considerar uma célula unitária bem grande e um grande espaço vazio entre as moléculas, chamado de slab, de forma que as moléculas de nitrogênio dentro da caixa não consigam interagir com as moléculas das caixas vizinhas. Além disso podemos fazer o cálculo considerando somente 1 k-point para x, y e z.

Em seguida, crie um gráfico com os valores da ligação no eixo \(x\) e os valores da energia total no eixo \(y\). Você deve obter um gráfico parecido com o mostrado abaixo:

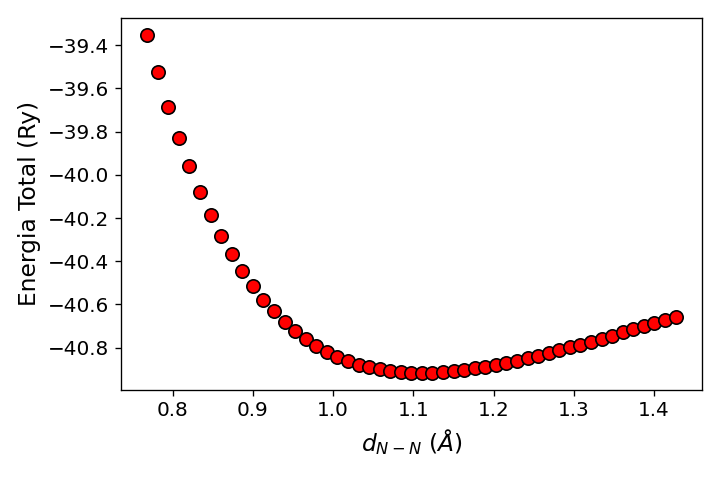
Figura 1: Energia em função da distância de ligação, \(E(d_{N-N})\) para a molécula de \(N_2\). Os pontos vermelhos são os valores calculados.

Modelando a SEP com um potencial harmônico

Podemos expandir a função energia total (\(U(x)\)) como uma série de Taylor, na forma:

\[U(x) = \sum_{n=0}^{\infty} \frac{E^{(n)}(x_0)}{n!} (x - x_0)^n \approx U(x_0) + U^\prime (x_0)(x - x_0) + \frac{1}{2} U^{\prime \prime} (x_0)(x - x_0)^2 + \frac{1}{6} U^{\prime \prime \prime} (x_0)(x - x_0)^3 + ...\]

Se considerarmos o caso em que temos valores de deslocamento muito próximos do valor de equilíbrio, i.e. \(x\approx x_0\), teremos \(U(x_0)=0\). Desconsiderando os termos de terceira ordem e de ordem superior, ficamos com:

\[U^{H}(x) = \frac{1}{2}k(x-x_0)^2 + U_0, \qquad U^{\prime \prime} (x_0) = k \quad e \quad U(x_0)=U_0\]

Essa é a equação de um oscilador harmônico. Esse é um modelo simplificado que é largamente utilizado para representar a ligação entre dois átomos, que é equivalente a considerar a ligação química como um sistema massa mola com constante de mola \(k\) oscilando em torno da distância de equilíbrio \(x_0\). Podemos tirar algumas informações úteis da curva apresentada na equação acima, com um certo tratamento desses dados.

1. Tente fazer um ajuste não linear da equação do oscilador harmônico. O ajuste ficou bom?

2. Tente agora fazer o ajuste não linear somente com os dados entre o 15° e 30° pontos. Melhorou ou piorou?

3. Qual o significado físico das constantes \(k\), \(U_0\) e \(x_0\)?

4. Por que fazer o ajuste entre o 15° e 30° resultou em um ajuste melhor do que considerando todos os pontos?

Como resultados do ajuste do potencial harmônico você deve obter um gráfico como o abaixo:

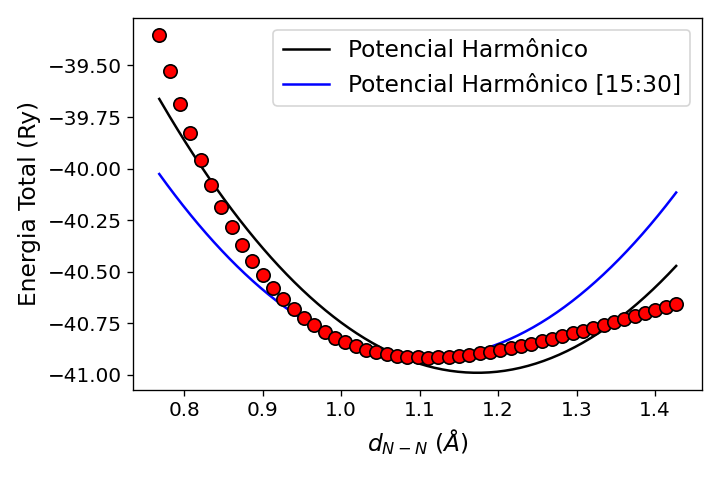
Figura 2: Energia em função da distância de ligação, \(E(d_{N-N})\) para a molécula de \(N_2\). Os pontos vermelhos são os valores calculados, a linha preta e a linha azul são os ajustes de um potencial harmônico com diferentes pontos considerados.

Modelando a SEP com um potencial de Morse

O potencial de Morse pode ser uma escolha mais conveniente para modelar a energia potencial da interação entre átomos e moléculas diatômicas. É uma aproximação mais realista para a estrutura vibracional e considera a anarmonicidade que ligações químicas reais apresentam. A equação da função de energia potencial de Morse é:

\[U^{M}(r) = D_e(1 - e^{-a(r - r_e)})^2 + U_0\]

onde \(r\) é a distância interatômica, \(r_e\) a distância de equilíbrio da ligação, \(D_e\) é a profundidade do poço de potencial (energia de dissociação + energia de ponto zero), \(a\) controla a “abertura” do poço, sendo \(a = \sqrt{k_e/2D_e}\) com \(k_e\) sendo a constante de força do oscilador e \(U_0\) a energia dos átomos infinitamente isolados.

1. Faça o ajuste do potencial de Morse nos dados calculados e obtenha a distância de equilíbrio e \(D_e\). Compare o \(d_{NN}\) obtido pelo ajuste com o valor experimental. Qual a discrepância relativa. O valor calculado é bom ou ruim?

2. Qual a constante de força do oscilador?

3. Compare o \(R^2\) e os dados obtidos do ajuste do oscilador harmônico e da equação de Morse. Qual se ajusta melhor? Que consequências podemos tirar desse resultado?

Como resultados do ajuste do potencial de Morse você deve obter um gráfico como o abaixo:

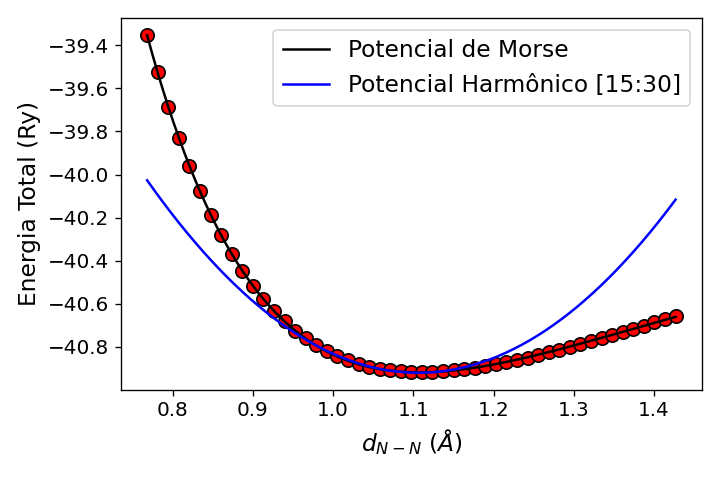
Figura 3: Energia em função da distância de ligação, \(E(d_{N-N})\) para a molécula de \(N_2\).

Obtendo informações físico-químicas a partir dos modelos para a SEP

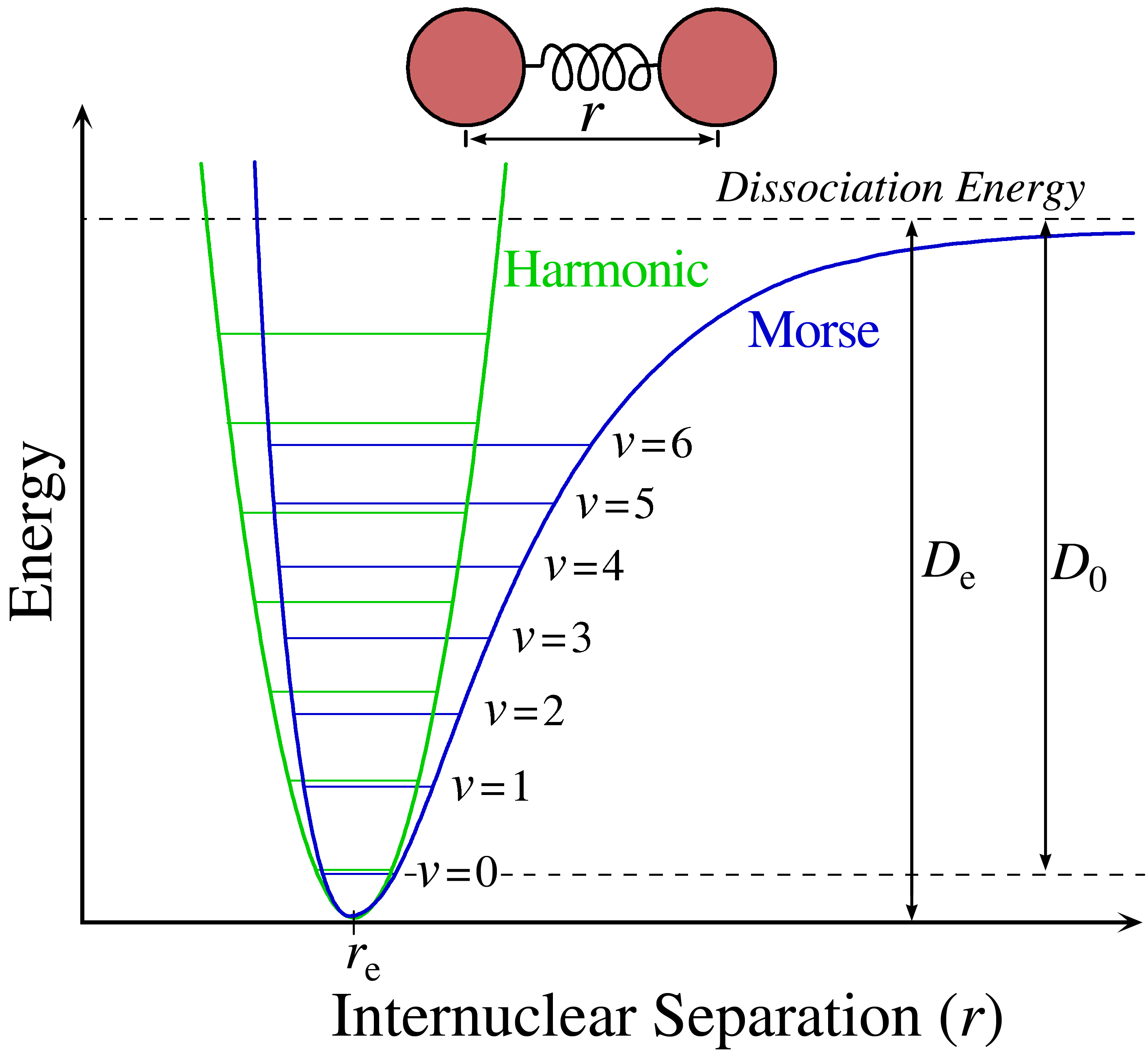
Figura 4: Comparação entre o potencial de Morse e o potencial Harmônico.

Calculando os modos vibracionais

Se olharmos para a Figura 4 é possível observar que o primeiro nível energético, chamado de \(\nu_0\) está levemente acima do mínimo da superfície de energia potencial. Essa diferença de energia é conhecida como energia de ponto zero.

A Energia de Ponto Zero (ZPE - Zero-Point Energy) é a diferença de energia entre o ponto mais baixo da superfície de energia potencial (energia eletrônica de equilíbrio) e a energia referente ao nível vibracional \(n=0\). Não é possível medir diretamente a ZPE, uma vez que não é possível observar a molécula no estado de menor energia da superfície de potencial. Sendo assim, o termo experimental ZPE descreve o valor que é usualmente derivado combinando constantes espectroscópicas experimentais e modelos para osciladores anarmônicos. Portanto, valores experimentais de ZPE são um híbrido entre experimento e modelo teórico.

Os níveis energéticos de um oscilador harmônico e anarmônico são dados por:

\[E_\nu^{H} = h\omega_0 \left(n + \frac{1}{2} \right), \qquad \omega_0 = \frac{1}{2\pi}\sqrt{\frac{k}{\mu}}\] \[E_\nu^{M} = h\omega_0 \left(n + \frac{1}{2} \right)\left[ 1 - \frac{h\omega_0}{4D_e} \left(n + \frac{1}{2} \right)\right]\]

Onde \(n\) é o número quântico vibracional. A energia de ponto zero (ZPE) é a energia obtida quando \(n = 0\).

1. Calcule \(\omega^H_0\) e \(\omega^M_0\).

2. O valor experimental para o estado fundamental(\(X^1\Sigma_g^+\)) da molécula de \(N_2\) é \(\omega_0 = 2329.92 \pm 3 cm^{-1}\). [4] Calcule a discrepância relativa entre os valores calculados \(\omega^H_0\) e \(\omega^M_0\) e o experimental.
   • Use \(c = 2.998\cdot 10^{10} cm.s^{-1}\) , \(1 Ry = 2.179872 \cdot 10^{-18} kg.m^2.s^{-2}\), \(1 u.m.a = 1.660538\cdot 10^{-27} kg\), \(h = 6.62607\cdot 10^{-34} m^2.kg.s^{-1}\)
3. Calcule a ZPE para o potencial harmônico e o potencial de Morse. Compare (discrepância relativa) com o valor “experimental” \(1175.78 \pm 5 cm^{-1}\) [5].

Calculando a energia de dissociação

A energia de dissociação \(D_0\) pode ser calculada como: \(D_0 = D_e - E_{ZPE}\).

1. Com base nos valores de \(D_e\) e da energia de ponto zero obtidas do modelo de Morse das etapas anteriores, calcule a energia de dissociação.
2. O valor experimental da energia de dissociação para o \(N_2\) é de \(225.07 \pm 0.11 kcal/mol\). [2] Qual a discrepância relativa entre o valor calculado e o valor experimental?
   • Use \(1 Ry = 1312.7497 kJ/mol = 313.7547 kcal/mol = 13.6057 eV, 1 eV = 8065.54 cm^-1\)

[1] BOWEN, Humphrey John Moule. Tables of interatonic distances and configuration in molecules and ions. 1958.

[2] VEDENEEV, Vladimir Ivanovich; VEDENEEV, Vladimir Ivanovich. Bond energies, ionization potentials, and electron affinities. London: E. Arnold, 1966.

[3] BARONI, Stefano et al. Phonons and related crystal properties from density-functional perturbation theory. Reviews of Modern Physics, v. 73, n. 2, p. 515, 2001.

[4] BENDTSEN, Jørgen. The rotational and rotation‐vibrational Raman spectra of \(^{14}N_2\), \(^{14}N^{15}N\) and \(^{15}N_2\). Journal of Raman Spectroscopy, v. 2, n. 2, p. 133-145, 1974.

[5] IRIKURA, Karl K. Experimental vibrational zero-point energies: Diatomic molecules. Journal of physical and chemical reference data, v. 36, n. 2, p. 389-397, 2007.

Respostas:

• Modelando a SEP com um potencial harmônico
  1. \(k = 16.168374\), \(x_0 = 1.173567\), \(U_0 = -40.99045\), \(R^2 = 0.923993\)
  2. \(k = 15.639469\), \(x_0 = 1.106218\), \(U_0 = -40.919649\), \(R^2 = 0.997115\)
  3. \(k\) é a constante de mola e, a grosso modo, está relacionado a quão forte é a ligação química. Lembre-se de que na equação da mola, \(k\) é a constante de proporcionalidade entre uma deformação \(\Delta x\) e a energia necessária para que essa deformação aconteça. Sendo assim, quando maior for o \(k\), maior será a energia necessária para que uma dada deformação do comprimento da ligação química ocorra. \(x_0\) é a posição de equilíbrio do oscilador harmônico, ou seja, a distância de equilíbrio da ligação química. \(U_0\) é a profundidade do poço de potencial, ou seja, a energia total da molécula na distância de equilíbrio.
• Modelando a SEP com um potencial de Morse
  1. \(D_e = 0.830694\), \(r_e = 1.107412\), \(a = 2.546868\), \(U_0 = -40.917764\), \(R^2 = 0.999988\), 1.15%}
  2. \[k_e = 10.38\]
• Calculando os modos vibracionais
  1. \(\omega^H_0 = 2375.3 cm^{-1}\) e \(\omega^M_0 = 2342.22 cm^{-1}\)
  2. 0.35 %, 1.95 % e 0.53 % 3.