Tutorial QE: Sistemas bidimensionais (2D)
Nesse tutorial aprenderemos:
- Como obter a geometria de equilíbrio de um sistema 2D;
- Como calcular por DFPT os modos vibracionais da estrutura;
- Fazer o gráfico de dispersão de fônons e comparar com valores obtidos experimentalmente;
Dentre os mais diversos sistemas 2D que podemos explorar, de longe o mais famoso e estudado na literatura é o grafeno. Ele apresenta dois átomos em uma célula unitária hexagonal, como representado na figura abaixo.
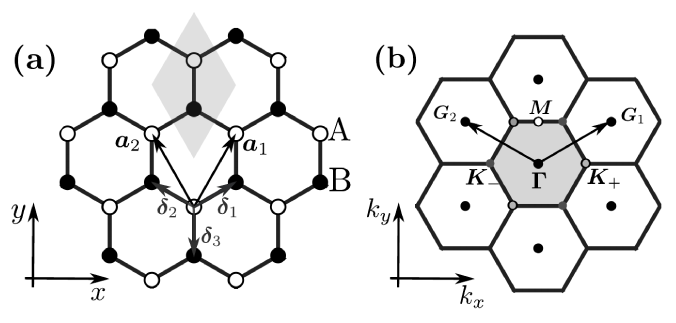
Figura 1: (a) Representação da célula unitária do grafeno e dos átomos não equivalentes. (b) Representação da primeira zona de Brillouin e os pontos de alta simetria.
Uma rede do tipo “honeycomb” não é uma rede de Bravais. A rede de Bravais do grafeno é uma rede hexagonal. Uma rede Bravais hexagonal é aquela cuja célula unitária é um prisma com bases hexagonais e cujos pontos de rede estão localizados nos vértices da célula unitária e nos centro da base. Apesar de comumente algumas pessoas se referirem ao grafeno como uma rede do tipo “honeycomb”, essa denominação está errada e não deve ser utilizada.
Podemos representar a célula unitária do grafeno de duas formas: (1) Um átomo posicionado no centro (0, 0, 0) e outro na posição (1/3, 2/3, 0); (2) Um átomo em (2/3, 1/3, 0) e outro em (1/3, 2/3, 0). Ambas são absolutamente equivalentes, entretanto a primeira representação apresenta simetria \(P\bar{6}m2\) #187 e a segunda \(P6/mmm\) #191 apresenando 24 elementos de simetria. Por isso, vamos utilizar a segunda forma de representar a estrutura.
Estrutura em equilíbrio
Assim como fizemos para moléculas, precisamos primeiramente obter a estrutura de equilíbrio para o sistema. Nesse caso, entretanto, não iremos variar a posição dos átomos, mas manter suas posições na célula unitária fixas e variar o parâmetro \(a\). Além disso, de maneira análoga como fizemos anteriormente utilizaremos um slab entre as folhas para que tenhamos um sistema 2D.
#!/bin/bash
CMD_PW="mpirun -np 4 /home/users/lipelopes/qe-6.4/bin/pw.x"
PREFIX="grafeno"
PSEUDO_DIR="/home/interlab/pseudo/"
CALC='scf'
for celldm in 4.181673 4.23058145 4.27948991 4.32839837 4.37730682
4.42621528 4.47512373 4.52403219 4.57294065 4.6218491 4.67075756
4.71966601 4.76857447 4.81748293 4.86639138 4.91529984 4.96420829
5.01311675 5.06202521 5.11093366
do
#Make SCF calculation
cat>$PREFIX.$celldm.$CALC.in<<EOF
grafeno1x1 - PW SCF calculation
&control
calculation = '$CALC' , restart_mode = 'from_scratch' ,
wf_collect = .false. , outdir = '.' ,
pseudo_dir = '$PSEUDO_DIR' , prefix = '$PREFIX' ,
/
&system
ibrav = 4 , celldm(1) = $celldm, celldm(3) = 10,
nat = 2 , ntyp = 1 ,
ecutwfc = 80.0 , ecutrho = 600.0 ,
/
&electrons
conv_thr = 1.0D-10 , electron_maxstep = 5000 ,
/
ATOMIC_SPECIES
C 12.0107 C.pbe-van_ak.UPF
ATOMIC_POSITIONS (crystal)
C 0.666666667 0.333333333 0.000000000
C 0.333333333 0.666666667 0.000000000
K_POINTS automatic
12 12 1 0 0 0
EOF
$CMD_PW < $PREFIX.$celldm.$CALC.in > $PREFIX.$celldm.$CALC.out
done
Vamos fazer um processo análogo ao feito para moléculas, entretanto dessa vez vamos automatizar um pouco o processo. No script grafeno.sh utilizamos um for para executar os cálculos sequencias para os diversos valores de parâmetros \(a\). No código run.py;, disponibilizado abaixo, escrevemos um script para abrir todos os arquivos *.out;, pegar as energias, fazer o ajuste do potencial de Morse e gerar o gráfico e devolver os parâmetros do ajuste de maneira totalmente automática. Facilita um pouco a vida, não é mesmo?
Para executar esse script você precisa ter instalado em seu computador o Python e todas as suas bibliotecas. Pessoalmente recomendo a utilização da distribuição Anaconda, que pode ser obtida aqui, com Python versão 3.7. Ela já vêm com diversas bibliotecas como matplotlib, numpy e scipy. Após instalar o Anaconda, basta abrir o programa Spyder, colocar o script abaixo, salva-lo na pasta que contém os arquivos .out e apertar F5 para executá-lo. Ele irá salvar o gráfico automaticamente em três formatos diferentes nesta pasta.
import os
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as sci
def anarmonic_p(x, De, re, a, D0):
'''Morse potential'''
return De*(1 - np.exp(-a*(x - re)))**2 + D0
def r_square_g(xs, ys, yteo):
'''Calculates the R² of the fit.'''
ymed = sum(ys)/len(ys)
SQtot = sum([(i-ymed)**2 for i in ys])
SQres = sum([(i-ymed)**2 for i in yteo])
return SQres/SQtot
def ajust(xdata, ydata, p0 = [0.8,4.6,2.57,-20]):
popt, pcov = sci.curve_fit(anarmonic_p, xdata, ydata, p0, method='dogbox')
r2 = r_square_g(xdata, ydata, anarmonic_p(xdata, *popt))
return anarmonic_p(xdata, *popt), r2, popt
list_output = [name_file for name_file in os.listdir(os.getcwd()) if '.out' in name_file]
d_NN = []
energias = []
for name in list_output:
d_NN += [float(name[8:-8])]
arquivo = open(os.path.join(os.getcwd(), name)).readlines()
e = [i for i in arquivo if '!' in i]
energias += [float(e[0][36:-5])]
aj = ajust(d_NN, energias)
print('De = %f, re = %f, a = %f, D0 = %f, R2= %f'
%(aj[-1][0], aj[-1][1], aj[-1][2], aj[-1][3], aj[-2]))
plt.plot(np.linspace(d_NN[0], d_NN[-1], 200),
anarmonic_p(np.linspace(d_NN[0], d_NN[-1], 200), *aj[-1]), color='black')
plt.plot(d_NN, energias, 'o', ms=8, lw=2, alpha=1, mfc='red', color='black')
plt.xlabel(r'$a$ ($\AA{}$)', fontsize=14)
plt.ylabel('Energia Total (Ry)', fontsize=14)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.tight_layout()
plt.savefig('plot.pdf')
plt.savefig('plot.png')
plt.savefig('plot.svg')
plt.show()
Como resultado do ajuste do potencial de Morse obtemos os parâmetros: \(D_e = 1.504019, r_e = 4.659226, a = 0.554086, D_0 = -24.857592, R^2= 1.000000\). Como resultado do ajuste do potencial harmônico obtemos os parâmetros: \(k = 0.887535, x_{0} = 4.663421, V_0 = -24.858048, R^2= 0.998246\).
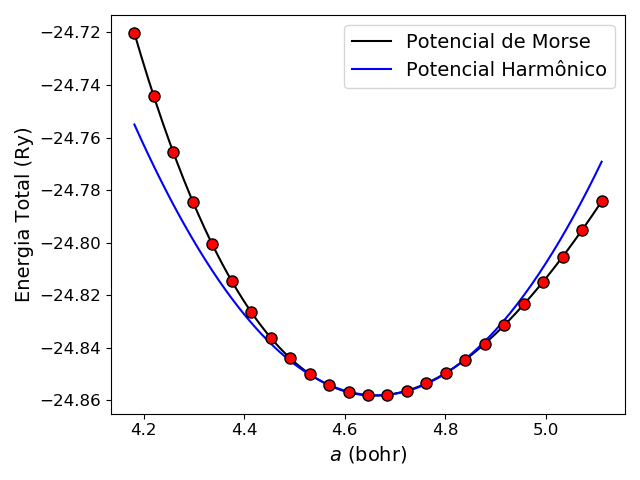
Figura 2: Energia em função do parâmetro \(a\) da célula unitária, \(E(a)\) para o grafeno. Os pontos vermelhos são os valores calculados e a linha preta um ajuste de um potencial de Morse e a linha azul o ajuste de um potencial harmônico.
Energia coesiva
Utilizando a regra de Hund, qual o termo espectroscópico do átomo de carbono isolado? Faça um cálculo spin polarizado e obtenha a energia do átomo de carbono isolado. Utilizando mesmo método utilizado para a molécula de \(N_2\), calcule a energia coesiva para o grafeno.
Dispersão de fônons
Para avaliar a estabilidade da estrutura devemos, da mesma forma como fizemos com a molécula de \(N_2\), olhar para os modos normais de vibração da estrutura. Entretanto, diferente de como fizemos anteriormente não vamos apenas fazer o cálculo em \(\Gamma\) (centro da zona de Brillouin), mas sim calcular como os modos normais de vibração variam ao longo de um caminho interligando os pontos de alta simetria da primeira zona de Brillouin. A zona de Brilluoin para o grafeno está ilustrada na Figura 1-(b), apresentando a primeira zona hachurada. Devido à simetria da estrutura temos de maneira geral três principais pontos de interesse: \(\Gamma\), \(K\) e \(M\).
O procedimento para esse cálculo é levemente mais complexo que o anterior e apresenta mais passos. Primeiro, temos que fazer um cálculo SCF da estrutura otimizada. Como o sistema é 2D, o comando assume_isolated='2D'; deve ser adicionado na tag &system; para considerar o sistema isolado e não termos problemas com o cálculo dos campos elétricos.[1] Eu recomendo que você crie uma nova pasta, com um nome como PhDisp e execute todos os cálculos nessa pasta, para evitar que ocorra confusão com os arquivos gerados pelos cálculos ateriores.
Em seguida vamos fazer o cálculo dos fônons de forma semelhante à feita anteriormente, mas agora em vez de fazer somente em \(\Gamma\), faremos em um grid de q-vetores (vetores de deslocamento da estrutura no espaço recíproco), utilizando o input abaixo crie o arquivo phgrid.sh. Esse cálculo pode levar bastante tempo, dependendo de quantos pontos iremos pegar utilizar no grid e quão simétrica a estrutura é. Cálculos desse tipo podem facilmente demorar semanas. Vamos fazer um grid de 8x8x1, ele é suficiente para obtermos um bom resultado. Perceba que assim como o grid de k-poins, também utilizamos somente um ponto em z, pois estamos considerando a estrutura 2D.
#!/bin/bash
CMD_PH="mpirun -np 4 /home/users/lipelopes/qe-6.4/bin/ph.x"
PREFIX="grafeno"
CALC='phG'
cat > $PREFIX.$CALC.in << EOF
&inputph
prefix='$PREFIX',
recover=.true.,
outdir='.' ,
ldisp=.true. ,
fildyn='$PREFIX.dyn' ,
nq1=8 , nq2=8 , nq3=1 ,
tr2_ph=1.0d-16,
/
EOF
$CMD_PH < $PREFIX.$CALC.in > $PREFIX.$CALC.out
Em seguida faremos o pós-processamento dos dados. Utilizando o script abaixo crie o arquivo phplot.sh e execute-o. Primeiro o programa q2r.x; gera as constantes de força no espaço real a partir da matriz dinâmica calculada no espaço dos q-vetores. Em seguida o programa matdyn.x; utiliza interpolação de Fourier para obter os valores dos modos vibracionais no caminho desejado na zona de Brillouin. Por fim o programa plotband.x; gera os dados em um formado que podemos fazer o gráfico de maneira um pouco mais fácil.
#!/bin/bash
Q2R_COMMAND="mpirun /home/users/lipelopes/qe-6.4/bin/q2r.x"
MATDYN_COMMAND="mpirun -np 8 /home/users/lipelopes/qe-6.4/bin/matdyn.x"
CMD_PLOT="mpirun /home/users/lipelopes/qe-6.4/bin/plotband.x"
PREFIX="grafeno"
# run q2r to calculate the interatomic force constants -
IFCs (in realspace) from the dynamical matrices (in q space)
cat > $PREFIX.q2r.in <<EOF
&input
fildyn='$PREFIX.dyn', flfrc='$PREFIX.fc', zasr='crystal',
/
EOF
$Q2R_COMMAND < $PREFIX.q2r.in > $PREFIX.q2r.out
# recalculate omega(q) from C(R) using matdyin through k-path
cat > $PREFIX.matdyn_disp.in <<EOF
&input
q_in_band_form=.true.,
loto_2d=.true., flfrc='$PREFIX.fc', flfrq='$PREFIX.freq',
asr='crystal',
/
4
0.0000000000 0.0000000000 0.0000000000 160 !G
0.5000000000 0.2886751300 0.0000000000 160 !M
0.6666666667 0.0000000000 0.0000000000 160 !K
0.0000000000 0.0000000000 0.0000000000 1 !G
EOF
$MATDYN_COMMAND < $PREFIX.matdyn_disp.in > $PREFIX.matdyn_disp.out
# Plotband
cat > $PREFIX.plotband.in <<EOF
$PREFIX.freq
-150 2000
freq.plot
freq.ps
0.0
200.0
0.0
EOF
$CMD_PLOT < $PREFIX.plotband.in > $PREFIX.plotband.out
Por fim vamos calcular a densidade de estados vibracionais por frequência com o programa matdyn.x;. Utilize o script abaixo para criar o arquivo phdos.sh e execute-o.
MATDYN_COMMAND="mpirun -np 8 /home/users/lipelopes/qe-6.4/bin/matdyn.x"
PREFIX="grafeno"
# run matdyn for DOS calculation
cat > $PREFIX.matdyn_ex.in <<EOF
&input
asr='crystal', flfrc='$PREFIX.fc',
flfrq='$PREFIX.freq', dos=.true.,
fldos='$PREFIX.phdos', deltaE=1.d0,
nk1=20, nk2=20, nk3=20,
/
EOF
$MATDYN_COMMAND < $PREFIX.matdyn_ex.in > $PREFIX.matdyn_ex.out
Ao final desse processo basta copiar os arquivos gerados para seu computador e executar o código em python disponibilizado abaixo que você deve obter um gráfico como o mostrado na Figura 3. Voltaremos a explorar a dispersão de fônons mais pra frente, explicando como obter os pontos de alta simetria no espaço recíproco, como fazer o gráfico e outros detalhes. Por hora, devemos nos concentrar apenas no fato de que, ao longo de todo o caminho no espaço recíproco, nenhuma frequência negativa apareceu. Isso indica que a estrutura é estável.
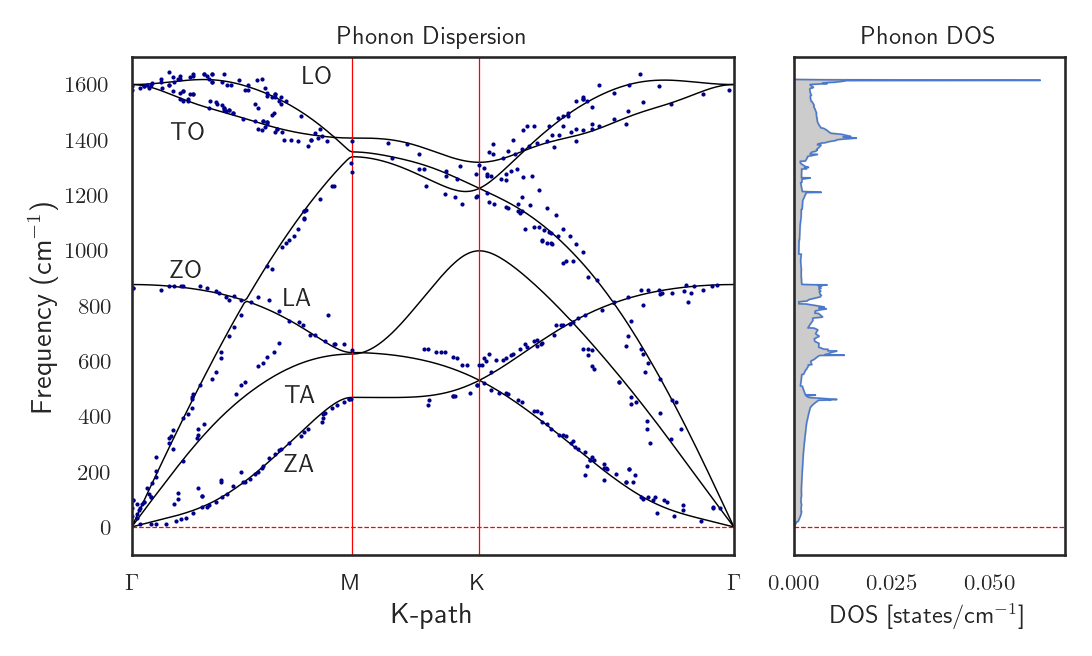
Figura 3: Gráfico da dispersão de fônons pelo k-path: \(\Gamma-M-K-\Gamma\) à esquerda e densidade de estados de vibracionais à direita. Os pontos azuis são os dados experimentais para o grafite adaptados de [2].
Abaixo você encontrará disponível o código para fazer esse gráfico de maneira automatizada.
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
prefix = 'grafeno'
sym_points = ['$\Gamma$', 'M','K','$\Gamma$']
def get_sym(prefix):
sym = []
temp = open(prefix+'.plotband.out', 'r').readlines()
for i in range(len(temp)):
if 'coordinate' in temp[i]:
temp[i] = temp[i].rstrip('\n')
temp[i] = temp[i].split(' ')
point = float(temp[i][-1])
if (point in sym) != True:
sym += [point]
return sym
def get_freq(prefix):
arquivo = 'freq.plot'
temp=open(arquivo, 'r')
bandsfile = temp.readlines()
temp.close()
bands=[]
for i in range(len(bandsfile)):
bandsfile[i] = bandsfile[i].rstrip('\n')
bandsfile[i] = bandsfile[i].lstrip(' ')
bandsfile[i] = bandsfile[i].split(' ')
if bandsfile[i] != ['']:
bands.append([float(bandsfile[i][0]),float(bandsfile[i][-1])])
k = []
for i in range(len(bands)):
if (bands[i][0] in k) == False:
k.append(bands[i][0])
k = np.array(k)
energy = [[]]*len(k)
for i in range(len(bands)):
for j in range(len(k)):
if bands[i][0]==k[j]:
energy[j] = energy[j] + [bands[i][1]]
e = [*zip(*energy)]
return k, e
def plot_freq(prefix, xlabel=['$\Gamma$', 'K', 'M', '$\Gamma$']):
k, e = get_freq(prefix)
HS = get_sym(prefix)
ymin, ymax = -100, 2500
for i in range(len(e)):
plt.plot(k,e[i], lw=1, color='black')
for i in HS[1:-1]:
plt.plot([i,i], [ymin,ymax], lw=.6, color='red')
plt.plot([min(k), max(k)], [0,0],'--', lw=.8, color='red')
plt.ylim([ymin,ymax])
plt.xlim(min(k), max(k))
plt.xticks(HS, xlabel, size=12)
plt.yticks(size=12)
plt.ylabel(r'Frequency (cm$^{-1}$)', size=14)
plt.xlabel('K-path', size=14)
plt.show()
def get_DOS(prefix):
dos = []
temp = open(prefix+'.phdos', 'r').readlines()[1:]
for i in range(len(temp)):
temp[i] = temp[i].rstrip('\n')
temp[i] = temp[i].split(' ')
dos += [[float(i) for i in temp[i] if i!='']]
return np.transpose(dos)[0:2]
def pltbandasDOS(prefix, xlabel, split=False):
k, energy = get_freq(prefix)
kpoints = get_sym(prefix)
ymin, ymax = -100, 1700
plt.figure(figsize = (16,12),dpi = 150)
ax1 = plt.subplot2grid((1,3), (0,0), colspan = 2)
ax2 = plt.subplot2grid((1,3), (0,2))
for i in range(len(energy)):
ax1.plot(k,energy[i],'-',ms=2.8,lw=0.7, color='black')
ax1.plot([kpoints[1:-1], kpoints[1:-1]],[ymin, ymax],lw=0.6,color='red')
ax1.axis([min(k), max(k), ymin, ymax])
ax1.plot([min(k), max(k)], [0,0],'--', lw=.6, color='red')
#PLOT EXPERIMENTAL DATA
try:
exp = open('exp_grafite.csv', 'r').readlines()
for i in range(len(exp)):
exp[i] = exp[i].rstrip('\n')
exp[i] = exp[i].split('>')
exp[i] = [float(exp[i][0]), float(exp[i][1])]
exp = np.transpose(np.array(exp))
ax1.plot(exp[0], exp[1], '.', color='darkblue', ms=2)
except:
print('Experimental data not found!')
ax1.text(0.4, 200, 'ZA', fontsize=12)
ax1.text(0.4, 450, 'TA', fontsize=12)
ax1.text(0.4, 800, 'LA', fontsize=12)
ax1.text(0.1, 900, 'ZO', fontsize=12)
ax1.text(0.1, 1400, 'TO', fontsize=12)
ax1.text(0.45, 1600, 'LO', fontsize=12)
ax1.set_ylabel(r'Frequency (cm$^{-1}$)', size=14)
ax1.set_xlabel('K-path', size=14)
ax1.set_xticks(kpoints)
ax1.set_xticklabels(xlabel)
ax1.set_title("Phonon Dispersion")
freq, dos = get_DOS(prefix)
ax2.plot(dos,freq, '-',color='b', lw=.7,label="Phonon DOS")
ax2.set_ylim(ax1.get_ylim())
ax2.set_xlim(min(dos), max(dos)*1.1)
ax2.plot([min(dos), max(dos)*1.1], [0,0],'--', lw=.6, color='red')
ax2.fill(dos , freq, alpha=0.4, color='gray')
ax2.set_yticks(())
ax2.set_title("Phonon DOS")
ax2.set_xlabel(r'vDOS [states/cm$^{-1}$]')
plt.savefig('fonon.pdf', dpi=150, transparent=False)
plt.savefig('fonon.png', dpi=150, transparent=True))
plt.show()
pltbandasDOS(prefix, xlabel=sym_points)
Os dados experimentais estão disponíveis aqui.
[1] SOHIER, Thibault; CALANDRA, Matteo; MAURI, Francesco. Density functional perturbation theory for gated two-dimensional heterostructures: Theoretical developments and application to flexural phonons in graphene. Physical Review B, v. 96, n. 7, p. 075448, 2017. PDF
[2] MOUNET, Nicolas; MARZARI, Nicola. First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives. Physical Review B, v. 71, n. 20, p. 205214, 2005. PDF


Leave a comment