Tratamento de Dados: Isotermas de adsorção - Introdução

Introdução

Medir a área superficial e o tamanho dos poros de um material em pó é uma tarefa consideravelmente difícil. Dentre as poucas técnicas disponíveis para tal missão, a mais amplamente utilizada é a adsorção de gases no sólido.

Ao longo desse tutorial, iremos explorar as diversas teorias que nos ajudam a obter dados relevantes utilizando diferentes teorias para tratar os dados.

BET

O método de BET [1], desenvolvido por Stephen Brunauer, Paul Hugh Emmett e Edward Teller, é um método para tratar dados de adsorção de gases (em geral N₂, mas pode ser estendido para virtualmente qualquer gás) e extrapolar valores para o volume de monocamada e, consequentemente, área específica de materiais porosos. Juntamente com outras técnicas, como t-plot e NLDFT, podemos determinar a área específica, externa e interna, de um sólido poroso disperso bem como a distribuição de tamanho e volume dos poros do material.

A Teoria

O método de BET é uma extensão a teoria de Langmuir e introduz o conceito de adsorção de multicamadas segundo três hipóteses adicionais:

1. As moléculas de gás irão adsorver fisicamente na superfície solida em camadas infinitas;
2. As diferentes camadas de adsorção não interagem entre sí;
3. A teoria se aplica a todas as camadas de adsorção.

Similar à teoria de Langmuir, o método de BET requer a suposição de mecanismos consequentes às três hipóteses consideradas, sendo elas>

1. A adsorção de cada molécula de gás na superfície do sólido está relacionada a uma única e bem definida energia de adsorção;
2. A única interação molecular considerável é a de que uma molécula poderá agir como sítio único de adsorção para outra molécula de uma nova camada;
3. A camada mais externa de adsorção está em equilíbrio com a fase gasosa — apresenta taxa de adsorção e dessorção similares;
4. O processo de dessorção é cineticamente limitado — calor de adsorção deve ser cedido;
   • Este fenômeno é homogêneo em todas as moléculas de uma mesma camada;
   • O calor de adsorção referente a primeira camada é igual a E1 — calor de adsorção à superfície sólida;
   • Assume-se que as demais camadas de adsorção são similares entre si e podem ser representadas como espécies condensadas — fase líquida —, portanto o calor de adsorção destas camadas é El — calor de liquefação;
5. Na pressão de saturação o número de camadas adsorvidas tende a infinito — equivalente a superfície sólida estar imersa em fase líquida.

Com base nas simplificações assumidas é possível desenvolver uma nova equação de isoterma para o modelo de múltiplas camadas derivada da teoria de monocamada. As equações obtidas são capazes de representar não só a forma geral de isotermas experimentais, mas predizer valores compatíveis médios para o calor de adsorção e o volume de gás necessário para completar a primeira camada de adsorção em um sólido. A equação resultante do método de BET, para infinitas camadas, pode ser expressa por:

\[v = \frac{v_m \cdot c \cdot p}{(p - p_0)[1 + (c - 1)(p/p_0)]}; \qquad c = e^\frac{(E_1 - E_L)}{RT}\]

onde \(v\) é o volume total de gás adsorvido, \(v_m\) é o volume de gás adsorvido quando a superfície do sólido está completamente coberta por uma monocamada, \(c\) é a constante de BET, \(p\) é a pressão medida no estado de equilíbrio, \(p_0\) é a pressão inicial do sistema. Podemos simplificar a anterior e reescreve-la na forma linearizada:

\[\frac{p}{v(p_0 - p)} = \frac{1}{v_m \cdot c} + \frac{c - 1}{v_m \cdot c} \frac{p}{p_0}\]

Essa equação é muito mais simples de se trabalhar e permite a obtenção dos parâmetros \(c\) e \(v_m\) com um simples ajuste linear dos dados, técnica conhecida como multi-point BET. Idealmente cinco medidas no intervalo de p/p0 entre 0.005 a 0.3 devem ser o suficiente para a determinação dos parâmetros. Os dados experimentais podem ser considerados aceitáveis quando \(R^2 \geq 0.9975\). Como resultado obtêm-se da interseção com o eixo das ordenadas \(1/v_mc\) e da inclinação da curva \((c-1)/v_mc\). Com as duas relações pode-se determinar \(v_m\) e \(c\), sendo o primeiro o volume de gás requerido para completar uma camada de adsorção e o segundo, por definição, aproximadamente \(exp[(E1-El)/RT]\). Uma vez conhecido \(v_m\) calcula-se a área específica de um material através da seguinte equação:

\[S^{BET} = \frac{v_m N_A \sigma_{gas}}{m}\]

onde \(S^{BET}\) é a área específica, \(N_A\) é o número de Avogadro, \(\sigma_{gas}\) é a área da seção transversal do gás adsorvido e \(m\) é a massa da amostra.

Analisando dados experimentais

O arquivo disponibilizado aqui contém os dados experimentais de adsorção de \(N_2\) a 77K em um material carbonáceo nanoporoso. Para esse material, considere \(p_0 = 765.23\) mmHg e \(m = 0.0142 \pm 0.0005\) g. Os dados apresentam os valores originais medidos pelo equipamento, sendo o volume adsorvido em unidades de \(cm^3\) e a pressão em mmHg.

Primeiramente, faça um gráfico como o mostrado na Figura 1. Fique atento às unidades do gráfico e às unidades dos dados fornecidos.

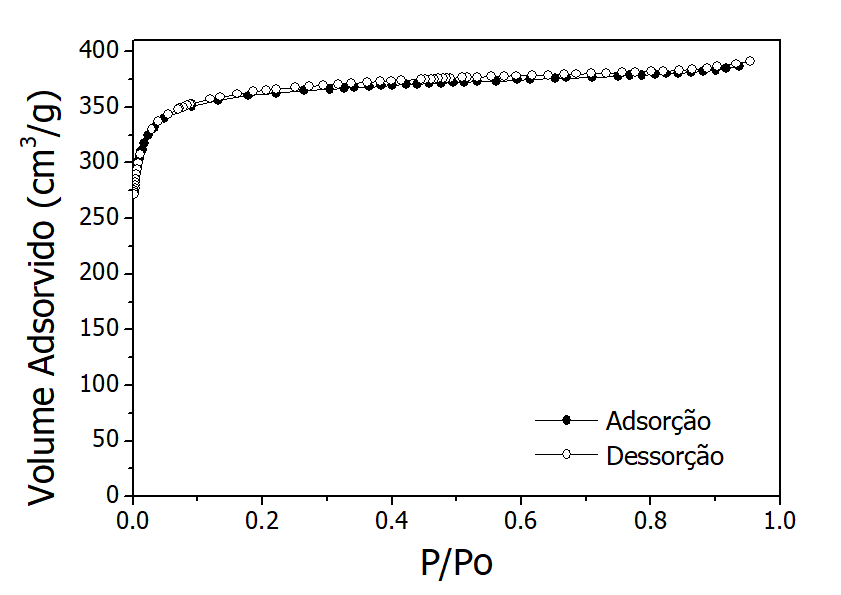
Figura 1: Isoterma de adsorção de N₂ a 77K em material microporoso carbonáceo.

É uma convenção representar a adsorção como símbolos cheios e a dessorção como símbolos vazios, ambos da mesma cor.

Agora utilize o método de linearização apresentado anteriormente e gere um gráfico como o abaixo. Localize o intervalo que em que ambos os parâmetros do ajuste linear sejam maiores que zero e o \(R^2 \geq 0.9975\).

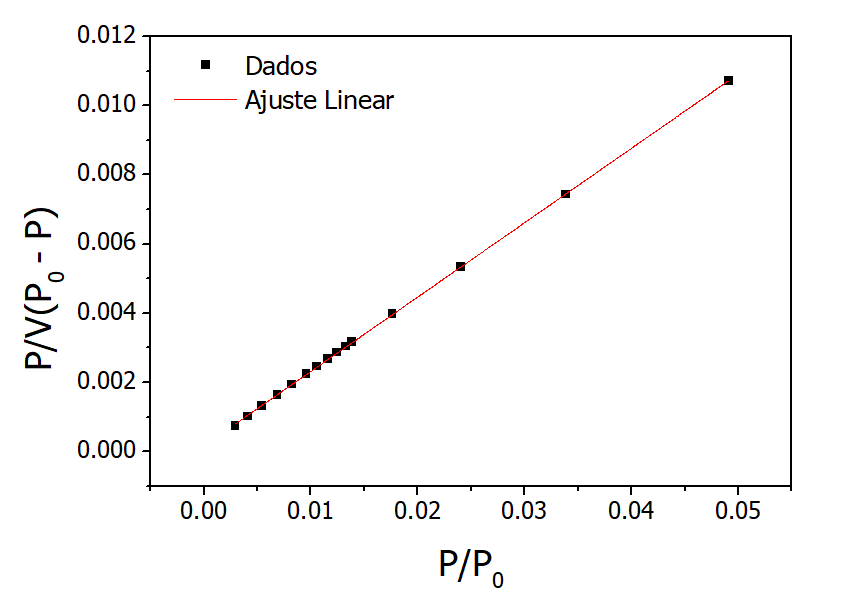
Figura 2: Gráfico de BET

Com base nos parâmetros do ajuste linear, determine a área específica deste material em unidades de \(m^2/g\). Utilize \(\sigma_{N_2} = 16.2 Å^2\) . Considerando a incerteza da medida da massa, qual a incerteza da área específica? Com base na constante \(c\), que conclusões podemos tirar?

[1] BRUNAUER, Stephen; EMMETT, Paul Hugh; TELLER, Edward. Adsorption of gases in multimolecular layers. Journal of the American chemical society, v. 60, n. 2, p. 309-319, 1938. 10.1021/ja01269a023 PDF