Tutorial QE: Sistemas unidimensionais (1D)
Nesse tutorial aprenderemos:
- Como obter a geometria de equilíbrio de maneira automática;
- Como calcular por DFPT os modos vibracionais;
- Comparar as energias relativas entre duas formas do carbino;
Vimos até agora como procurar por mínimos na superfície de potencial de maneira manual. Essa é uma maneira extremamente robusta de busca por estruturas estáveis, além de permitir a obtenção de uma grande quantidade de informações com um tratamento simples dos dados obtidos. Os casos que vimos até agora foram relativamente simples, uma vez que pudemos construir a superfície de potencial variando apenas um parâmetro.
Pense agora em um sistema levemente mais complexo, como o grafite por exemplo, que apresenta dois parâmetros da célula unitária. A superfície de energia potencial agora será não mais uma função de uma variável apenas, mas sim uma função 2 variáveis, os parâmetros \(a\) e \(c\) da célula unitária. Sistemas ainda mais complexos onde não só os parâmetros da célula unitária podem variar, mas também os comprimentos de ligação entre os átomos irão gerar uma hipersuperfície de energia potencial com \(n\) dimensões, onde \(n\) é o número de graus de liberdade do sistema. Nesses casos não é nada trivial buscar mínimos nesse tipo de função.
Para nossa sorte, existem diversos algoritmos automatizados para buscar mínimos em hipersuperfícies de energia potencial. Vamos utilizar o algorítmo BFGS quasi-newton. Ele é um algoritmo simples e poderoso, que em breve pretendo explorar com mais detalhes em um post exclusivo.
Carbino
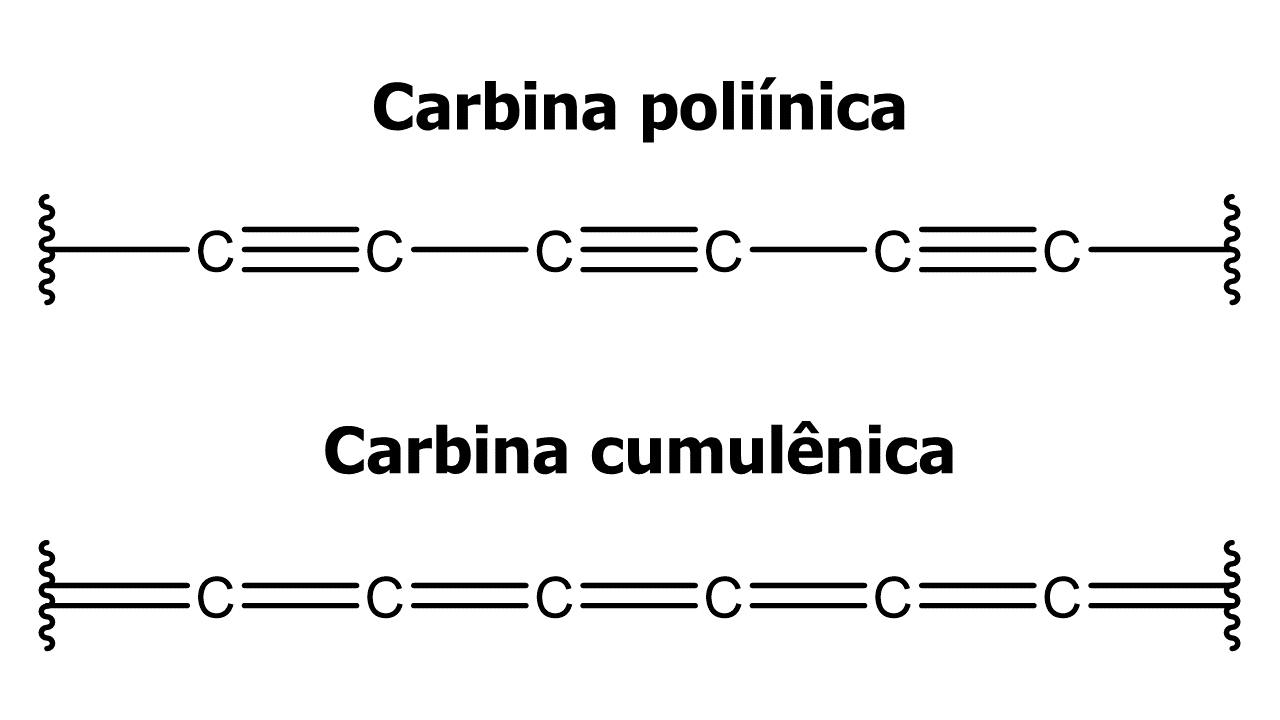
Figura 1: Diferentes estruturas da carbina.
A carbina é um alótropo de carbono formado por átomos de carbono sp ligados em uma única dimensão. Existe uma acalorada discussão na literatura se essa estrutura já foi obtida experimentalmente ou não. Além disso, podemos escrever duas estruturas diferentes para a carbina, a forma poliínica (-C≡C-)n e a forma cumulênica (=C=C=)n. Com a recente observação experimental do cyclo[18]carbon [1], um alótropo de carbono formado por um “anel” de carbina com 18 átomos, mais do que nunca os cálculos teóricos podem fornecer informações relevantes sobre esse tipo de sistema.
Carbino cumulênico
Vamos começar obtendo a estrutura da carbino cumulênico. Vamos montar uma célula unitária tetragonal, com \(x\) e \(y\) apresentando um slab bem grande, para evitarmos interação entre as cadeias, e os átomos no eixo \(z\). Como estamos considerando os comprimentos de ligação iguais, vamos colocar os átomos nas posições (0.5, 0.5, 0.25) e (0.5, 0.5, 0.75). A princípio os átomos poderiam ser colocados em qualquer posição da célula unitária, mas dessa forma nos aproveitamos da simetria do sistema para acelerar o cálculo. Segue a abaixo o input para executar cálculo. Como o sistema é pequeno e com poucos átomos, vamos apertar bastante os parâmetros para não termos problemas de convergência.
&control
calculation = 'vc-relax' ,
restart_mode = 'from_scratch' ,
wf_collect = .false. ,
outdir = '.' ,
pseudo_dir = '/home/pseudo' ,
prefix = '$PREFIX' ,
nstep=1000 ,
etot_conv_thr = 1.0d-4 , forc_conv_thr = 1.0d-5 ,
verbosity ='high' ,
tstress = .true. , tprnfor = .true. ,
/
&system
ibrav= 6,
celldm(1) = 15
celldm(3) = 0.322847788
nat = 2 , ntyp = 1 ,
ecutwfc = 120.0 , ecutrho = 1000.0 ,
/
&electrons
conv_thr = 1.0D-10 , electron_maxstep = 5000 ,
/
&IONS
ion_dynamics = 'bfgs'
/
&CELL
cell_dynamics = 'bfgs' , cell_dofree = 'z'
/
ATOMIC_SPECIES
C 12.0107 C.pbe-n-rrkjus_psl.0.1.UPF
ATOMIC_POSITIONS (crystal)
C 0.50000000 0.50000000 0.25000000
C 0.50000000 0.50000000 0.75000000
K_POINTS automatic
1 1 36 0 0 0
Perceba agora modificamos o tipo de cálculo para vc-relax, onde tanto os parâmetros de célula quanto os átomos podem relaxar suas posições. Nesse caso, como é um sistema 1D, permitimos somente que a célula unitária relaxe no eixo \(z\), adicionando na tag &CELL o parâmetro cell_dofree='z' para que somente o eixo z possa ter liberdade. Ambos átomos e parâmetros de célula devem sempre apresentar a mesma dinâmica de movimentos, que é definida pelo algoritmo bfgs de busca de mínimos na superfície de energia potencial. Após o cálculo obteremos então o resultado abaixo:
! total energy = -23.76675019 Ry
...
CELL_PARAMETERS (alat= 15.00000000)
1.000000000 0.000000000 0.000000000
0.000000000 1.000000000 0.000000000
0.000000000 0.000000000 0.322608697
ATOMIC_POSITIONS (crystal)
C 0.500000000 0.500000000 0.250000216
C 0.500000000 0.500000000 0.749999784
Veja que os átomos apresentaram um pequeno deslocamento no eixo \(z\), que é absolutamente irrelevante. O parâmetro \(z\) obtido foi 4.8391 bohr = 2.5601 Å. Ou seja, obtemos um comprimento das ligações cumulênicas de 1.2804 Å.
Precisamos agora calcular os modos normais de vibração, para ter certeza que essa estrutura corresponde a um mínimo local ou é um ponto de cela. Basta executar um cálculo SCF com a estrutura em equilíbrio obtida e, em seguida, executar os scripts abaixo. O primeiro realiza o cálculo dos fônons usando a Density-Functional Perturbation Theory e o segundo aplica a regra da soma acústica na matriz dinâmica para um sistema 1D.
PREFIX="carbina"
PSEUDO_DIR="/home/interlab/felipe/Pseudo"
CMD_PH="mpirun -np 8 /home/interlab/qe-6.4.1/bin/ph.x -nk 2"
CMD_DYNMAT="/home/interlab/qe-6.4.1/bin/dynmat.x"
cat>$PREFIX.phG.in<<EOF
phonons on a grid
&inputph
prefix='$PREFIX',
recover=.true.
fildyn='$PREFIX.dyn.G',
tr2_ph=1.0d-14,
asr=.true.,
/
0.0 0.0 0.0
/
EOF
$CMD_PH < $PREFIX.phG.in > $PREFIX.phG.out
#Make DynMat Acoustic Sum Rules calculation
cat>$PREFIX.asr.in<<EOF
$PREFIX - Acoustic Sum Rules - DynMat
&input
fildyn ='$PREFIX.dyn.G' ,
asr='one-dim' ,
/
EOF
$CMD_DYNMAT < $PREFIX.asr.in > $PREFIX.asr.out
Como resultando você deve obter o arquivo carbina.asr.out com os dados:
IR activities are in (D/A)^2/amu units
# mode [cm-1] [THz] IR
1 -0.00 -0.0000 0.0000
2 0.00 0.0000 0.0000
3 0.00 0.0000 0.0000
4 487.50 14.6148 0.0000
5 487.50 14.6148 0.0000
6 1502.36 45.0398 0.0000
Nele vemos as frequências dos modos vibracionais e a intensidade de absorção de IR. Como todos os modos são simétricos, nenhum deles apresenta atividades de IR. Podemos utilizar o XCrysDen para visualizar os vetores de deslocamento referentes a cada vibração. Basta abrir o arquivo dynmat.axsf e ir em Display > Forces.
Abaixo é possível conferir a representação visual de cada modo vibracional.
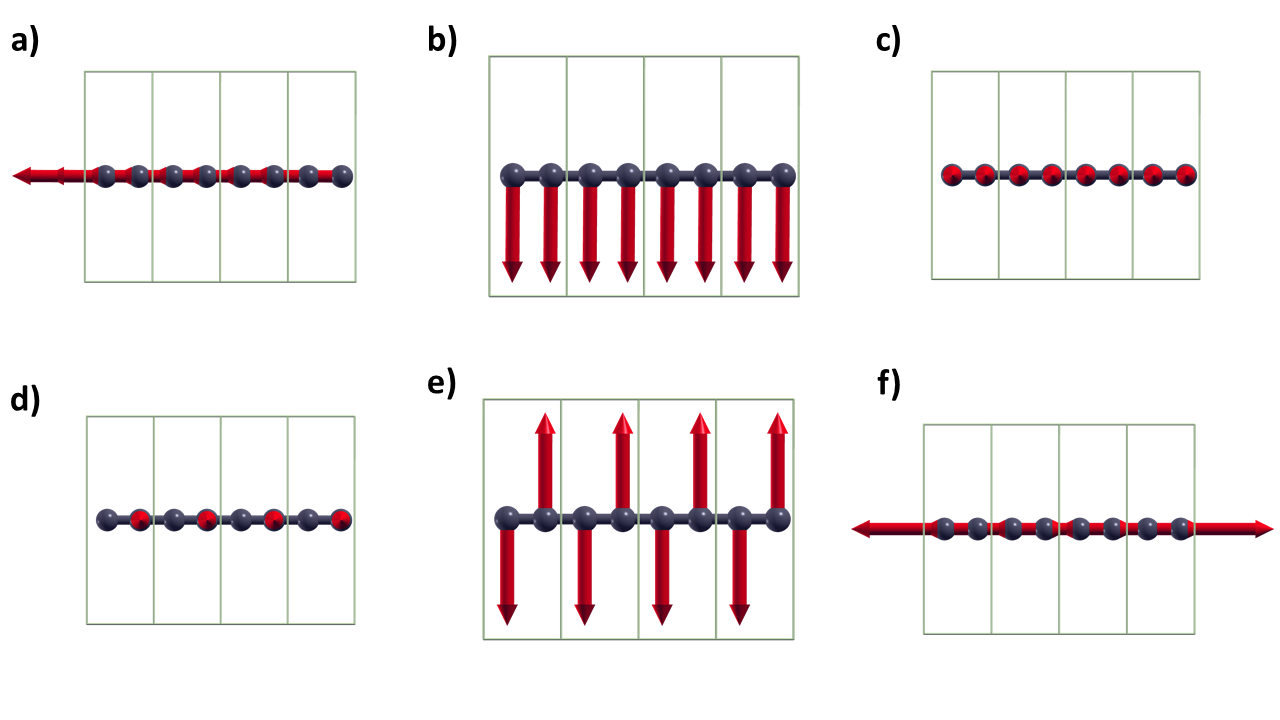
Figura 2: Os 6 modos vibracionas da carbina.
Perceba que os 3 primeiros são apenas translações de todos os átomos, por isso sua frequência é 0.
Carbina poliínica
Para obter a forma poliínica precisamos quebrar a simetria do sistema, deslocando um pouco os átomos. Vamos colocar os átomos nas posições (0.5, 0.5, 0.2) e (0.5, 0.5, 0.8) e executar o mesmo cálculo que fizemos anteriormente para relaxar a estrutura.
O resultado agora será
! total energy = -23.76759879 Ry
...
CELL_PARAMETERS (alat= 15.00000000)
1.000000000 0.000000000 0.000000000
0.000000000 1.000000000 0.000000000
0.000000000 0.000000000 0.322823627
ATOMIC_POSITIONS (crystal)
C 0.500000000 0.500000000 0.204433969
C 0.500000000 0.500000000 0.695566031
Obtemos agora \(z\) = 2.56246 Å e dois tipos de ligação, uma com 1.25851 Å e outra com 1.30396 Å. Calculando os modos vibracionais obtemos:
# mode [cm-1] [THz] IR
1 -0.00 -0.0000 0.0000
2 -0.00 -0.0000 0.0000
3 -0.00 -0.0000 0.0000
4 492.41 14.7619 0.0000
5 492.41 14.7619 0.0000
6 1591.52 47.7127 0.0000
Vemos aqui o mesmo padrão de modos vibracionais, 3 translacionais, 2 referentes à distorções e 1 referente à vibração no eixo das ligações. Podemos perceber também que as frequências são levemente mais altas, devido ao menor comprimento de uma das ligações que necessita de mais energia para ser deformada.
Por fim, podemos comparar as energias de ambas as estruturas. A forma cumulênica apresenta -23.76675019 Ry e a forma poliínica apresenta -23.76759879 Ry. Isso representa uma diferença de 0.26625 kcal/mol entre as duas conformações, sendo a forma poliínica a mais estável.
Essa diferença é relevante, porém pequena. Se considerarmos a energia térmica média, algo em torno de 0.6 kcal/mol, vemos que essa diferença é absolutamente desprezível.
Lembre-se que a energia total de um sistema calculado com pseudopotenciais não têm nenhum significado absoluto. Somente diferenças de energia apresentam uma interpretação física.
[1] KAISER, Katharina et al. An sp-hybridized molecular carbon allotrope, cyclo [18] carbon. Science, v. 365, n. 6459, p. 1299-1301, 2019. PDF


Leave a comment