Tutorial QE: Sistemas tridimensionais (3D)
Nesse tutorial aprenderemos:
- Como obter a geometria de equilíbrio de um sistema 3D;
- Obter o módulo Bulk do sólido a partir do ajuste da função de estado de Murnaghan;
- Fazer o gráfico de dispersão de fônons e comparar com valores obtidos experimentalmente;
Estrutura de equilíbrio
Por fim, para explorarmos um sistema 3D, vamos estudar a estrutura do diamante. Formado por uma célula primitiva cúbica de face centrada com grupo espacial \(F\bar{d}3m\) o diamante apresenta somente dois átomos não equivalentes nas posições (0,0,0) e (1/4, 1/4, 1/4). Monte o input para o cálculo da otimização da célula unitária para os parâmetros \(a\) assumindo os valores de 98% até 102% do valor obtido experimentalmente de 3.56679 Å (não se esqueça que o QE utiliza valores em unidades de bohr). Olhe no site com as informações do input do pw.x, que pode ser acessado aqui qual o ibrav para uma célula unitária cúbica de face centrada e monte o input do cálculo das energias, como feito para o grafeno. Construa o gráfico \(E(a)\) e ajuste uma parábola dos dados, você deverá obter um gráfico como o da Figura 1. Não esqueça que 1 Å = 1.88973 bohr!
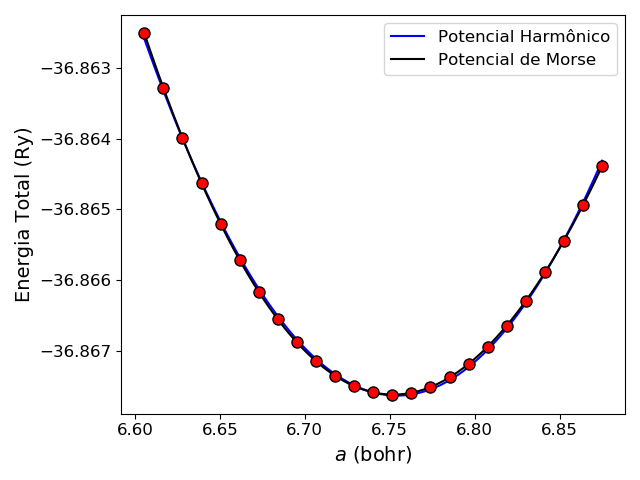
Figura 1: Energia em função do parâmetro \(a\) da célula unitária, \(E(a)\), para o diamante. Os pontos vermelhos são os valores calculados a linha preta o ajuste de um potencial de Morse e a linha preta um ajuste de um potencial harmônico. Perceba como, nesse caso, o potencial harmônico foi virtualmente tão bom quanto o potencial de Morse.
Módulo Bulk
Calculando por aproximação
O módulo Bulk de um material macroscópico isotrópico é definido à temperatura constante como:
\[B = \Omega_0 \left[\frac{\partial^2 u}{\partial \Omega^2}\right]_ {\Omega = \Omega_0}\]onde \(\Omega\) é o volume por átomo, \(\Omega_0\) é o volume por átomo no equilíbrio e \(u\) é a energia por átomo.
Com base nos dados do ajuste ne um potencial de Morse e de um potencial harmônico, qual o parâmetro de célula de equilíbrio? Qual a discrepância relativa com o valor obtido experimentalmente? R = alat\(^M\) = 6.752035, 0.21% , alat\(^H\) = 6.752322, 0.21%
Faça um gráfico E\(_ a\)(V\(_ a\)), onde E\(_ a\) é a energia por átomo e V\(_ a\) é o volume da célula unitária por átomo, e ajuste a equação de uma parábola. Utilizando os parâmetros obtidos pelo ajuste da parábola, calcule o módulo Bulk do diamante. Muita atenção nas unidades!!!
Use 1 Ry = 2.1798 10\(^{-18}\) N/m e 1 Pa = 1 N/m\(^2\)
R = a = 0.000393, b = -0.030328, c = -17.849320, R²= 0.997885, B = 446.16 GPa
O valor experimental é de 442 GPa [1]. Qual a discrepância relativa dos dados calculados para o dado experimental? R: 0.94%
Calculando através do ajuste da equação de estado de Murnaghan
Um tratamento mais completo pode ser feito utilizando a equação de estado de Murnaghan [2], que assume que o módulo Bulk é uma função linear da pressão na forma
\[B = B_0 + PB'_ 0\]E assim, para \(B'_ 0 \neq 0\), podemos escrever
\[E(V) = E_0 + B_0V_0 \left[ \frac{1}{B'_ 0(B'_ 0 - 1)} \left(\frac{V}{V_0}\right)^{1 - B'_ 0} + \frac{1}{B_0}\frac{V}{V_0} - \frac{1}{B'_ 0 - 1} \right]\]Faça um ajuste da equação de Murnaghan nos dados calculados e compare o módulo Bulk obtido por essa metodologia como o obtido do ajuste da equação da parábola e o valor experimental. Qual metodologia é a melhor?
Dispersão de fônons
Faça um cálculo SCF para o diamante com o valor de \(a\) de equilíbrio obtido anteriormente, modifique o script utilizado para calcular a dispersão de fônons do grafeno e o utilize para calcular a dispersão de fônons no diamante. Calcule em um grid de q-vetores de 4x4x4, seguindo o caminho \(\Gamma\)-X-K-\(\Gamma\)-L-X-W-L no espaço recíproco:
#!/bin/bash
CMD_PH="mpirun -np 4 /home/users/lipelopes/qe-6.4/bin/ph.x"
PREFIX="diamante"
CALC='phG'
cat > $PREFIX.$CALC.in << EOF
&inputph
prefix='$PREFIX',
recover=.true.,
outdir='.'
ldisp=.true. ,
fildyn='$PREFIX.dyn' ,
nq1=4 , nq2=4 , nq3=4 ,
tr2_ph=1.0d-16,
/
EOF
$CMD_PH < $PREFIX.$CALC.in > $PREFIX.$CALC.out
Em seguida faça o pós-processamento dos dados.
Q2R_COMMAND="mpirun /home/users/lipelopes/qe-6.4/bin/q2r.x"
MATDYN_COMMAND="mpirun -np 8 /home/users/lipelopes/qe-6.4/bin/matdyn.x"
CMD_PLOT="mpirun /home/users/lipelopes/qe-6.4/bin/plotband.x"
PREFIX="diamante"
# run q2r to calculate the interatomic force constants -
IFCs (in realspace) from the dynamical matrices (in q space)
cat > $PREFIX.q2r.in <<EOF
&input
fildyn='$PREFIX.dyn', flfrc='$PREFIX.fc', zasr='crystal',
/
EOF
$Q2R_COMMAND < $PREFIX.q2r.in > $PREFIX.q2r.out
# recalculate omega(q) from C(R) using matdyin through k-path
cat > $PREFIX.matdyn_disp.in <<EOF
&input
q_in_band_form=.true., flfrc='$PREFIX.fc',
flfrq='$PREFIX.freq', asr='crystal',
/
10
0.00000000 0.00000000 0.00000000 120 !gG
0.00000000 1.00000000 0.00000000 0 !X
1.00000000 1.00000000 0.00000000 120 !X
0.75000000 0.75000000 0.00000000 120 !K
0.00000000 0.00000000 0.00000000 120 !gG
0.50000000 0.50000000 0.50000000 120 !L
0.00000000 1.00000000 0.00000000 0 !X
1.00000000 1.00000000 0.00000000 120 !X
0.50000000 1.00000000 -0.00000000 120 !W
0.50000000 0.50000000 0.50000000 120 !L
EOF
$MATDYN_COMMAND < $PREFIX.matdyn_disp.in > $PREFIX.matdyn_disp.out
# Plotband
cat > $PREFIX.plotband.in <<EOF
$PREFIX.freq
-150 2000
freq.plot
freq.ps
0.0
200.0
0.0
EOF
$CMD_PLOT < $PREFIX.plotband.in > $PREFIX.plotband.out
Por fim vamos calcular a densidade de estados vibracionais por frequência com o programa matdyn.x;. Utilize o script abaixo para criar o arquivo phdos.sh e execute-o.
MATDYN_COMMAND="mpirun -np 8 /home/users/lipelopes/qe-6.4/bin/matdyn.x"
PREFIX="diamante"
# run matdyn for DOS calculation
cat > $PREFIX.matdyn_ex.in <<EOF
&input
asr='crystal', flfrc='$PREFIX.fc',
flfrq='$PREFIX.freq', dos=.true.,
fldos='$PREFIX.phdos', deltaE=1.d0,
nk1=20, nk2=20, nk3=20,
/
EOF
$MATDYN_COMMAND < $PREFIX.matdyn_ex.in > $PREFIX.matdyn_ex.out
Abaixo, você pode observar o resultado do cálculo, comparado com valores experimentais obtidos de [3] e [4].
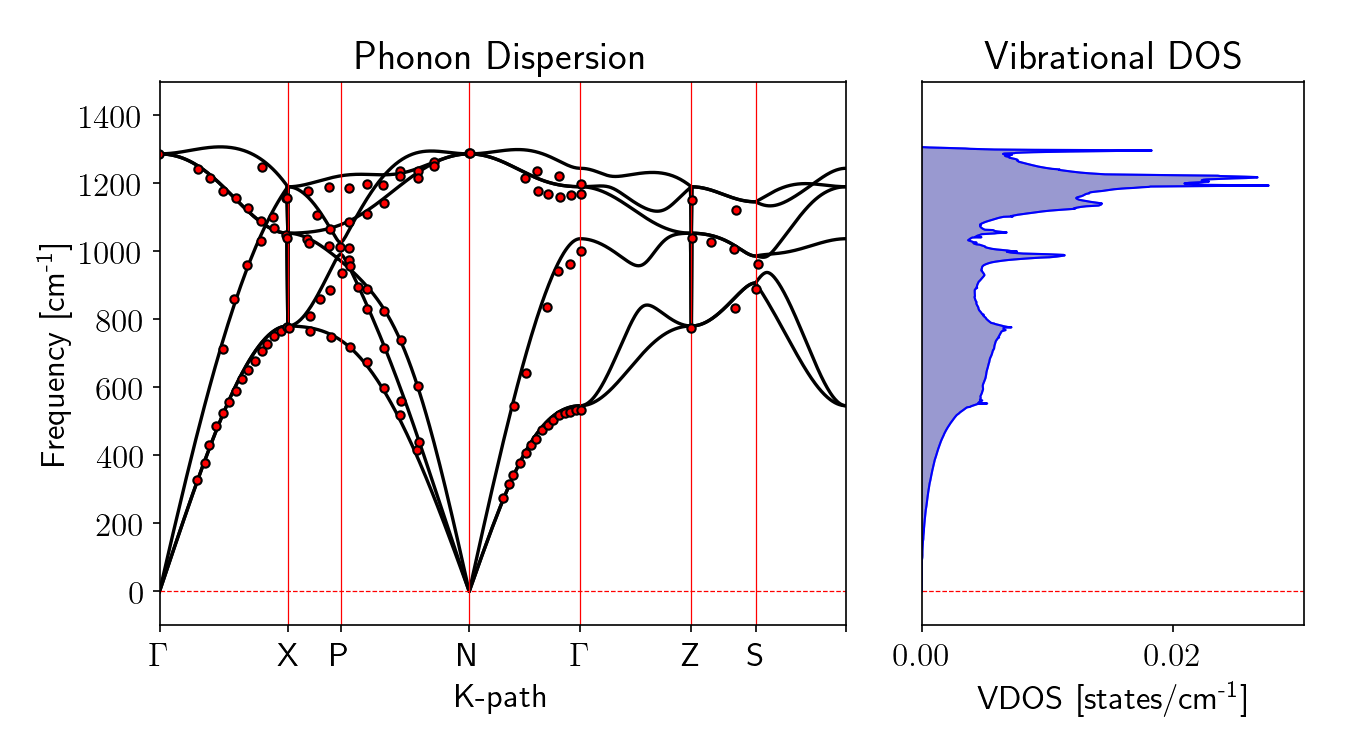
Figura 2: Gráfico da dispersão de fônons pelo k-path: \(\Gamma-X-K-\Gamma-L-X-W-L\) à esquerda e densidade de estados de vibracionais à direita. Os pontos vermelhos são os dados experimentais para o diamante retirados de [3] e [4].
Os dados experimentais estão disponíveis aqui.
[2] WARREN, J. L. et al. Lattice dynamics of diamond. Physical Review, v. 158, n. 3, p. 805, 1967.
[3] PAVONE, P. et al. Ab initio lattice dynamics of diamond. Physical Review B, v. 48, n. 5, p. 3156, 1993.PDF


Leave a comment